使用旧金山湾区地图学习 Cypher
场景和用例
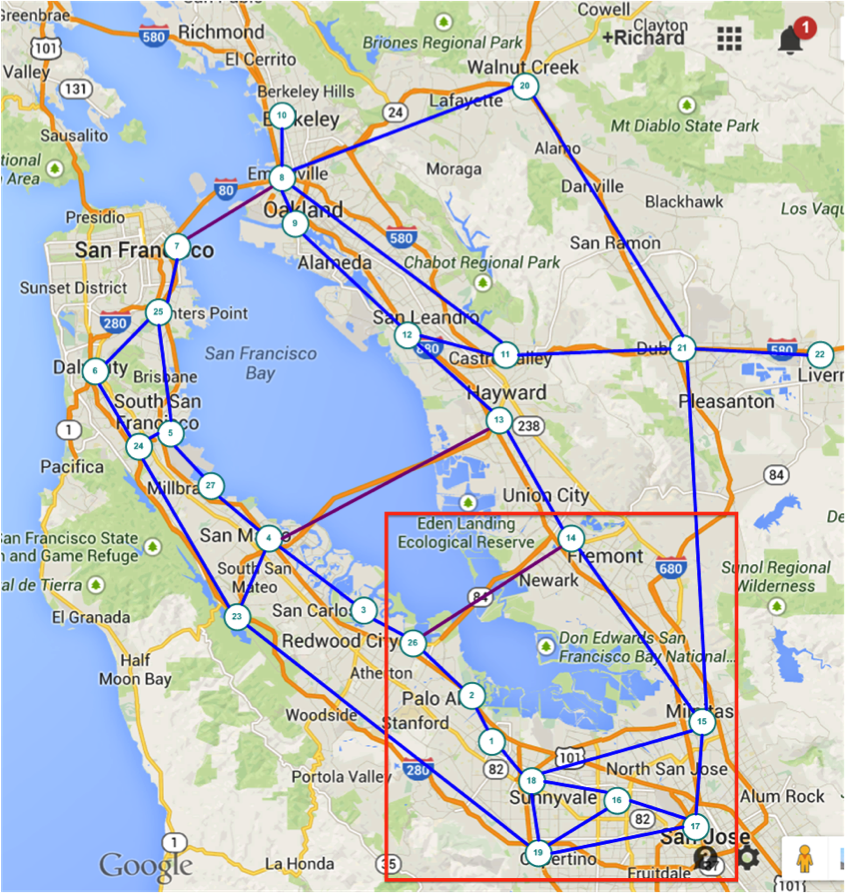
我们很多人每天都使用谷歌地图服务来查找从点 A 到点 B 的最佳路线、是否存在替代方案、哪种方式最快或最便宜。受最初的图论问题启发:"莱昂哈德·欧拉 (Leonhard Euler) 于 1736 年发表的关于柯尼斯堡七桥问题的论文被认为是图论史上的第一篇论文",我将使用简化的旧金山湾区道路地图来回答一些问题。在我的图中包含 3 座桥梁,将来我也许能提出更多有趣的问题。

我选择了一些主要城镇和连接它们的公路。为简单起见,最初我将只输入部分数据来开始学习。
模型
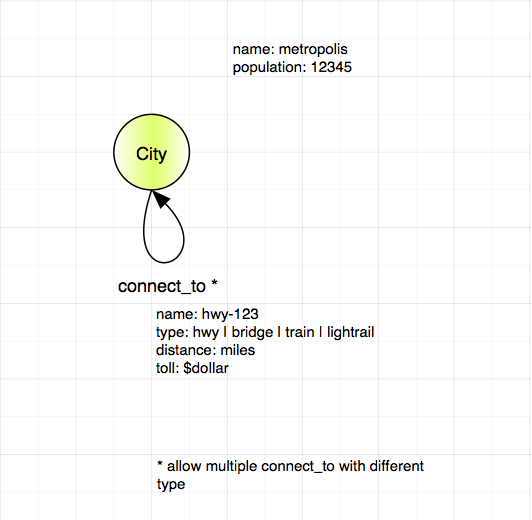
我从一个简单的模型开始,只包括节点(城市)和链接(公路)。
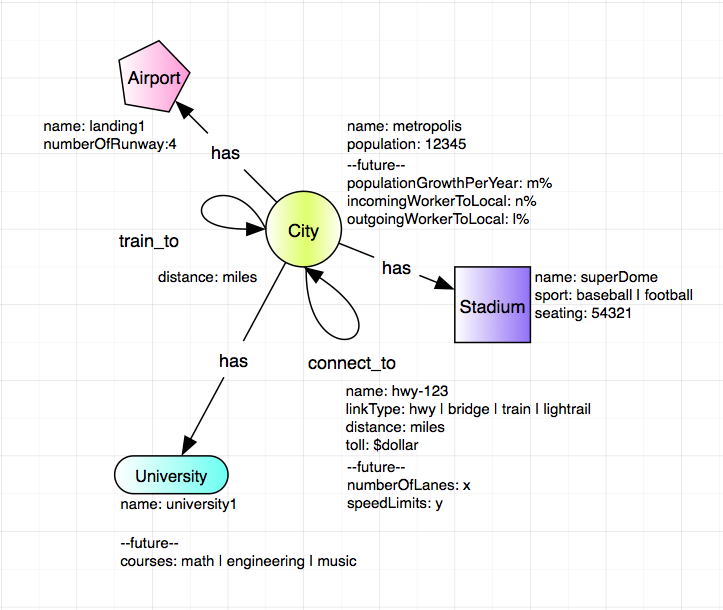
然后我添加了更多地点,如大学、体育场和机场,并与城市建立 [:has] 关系。
CREATE (n01:City {name: 'Mountain View', population: 77646}),
(n02:City {name: 'Palo Alto', population: 66642}),
(n18:City {name: 'Sunnyvale', population: 147559}),
(n14:City {name: 'Fremont', population: 224922}),
(n15:City {name: 'Milpitas', population: 69783}),
(n16:City {name: 'Santa Clara', population: 120245}),
(n17:City {name: 'San Jose', population: 998537}),
(n19:City {name: 'Cupertino', population: 60189}),
(n26:City {name: 'Athetron', population: 7159}),
(n01)-[:connect_to {distance: 5.5}]->(n02), // mtv - pa
(n01)-[:connect_to {distance: 2.9}]->(n18), // mtv - snyl
(n02)-[:connect_to {distance: 4.2}]->(n26), // pa - atht
(n26)-[:connect_to {distance: 17.1, linkType: 'bridge', toll: 0}]->(n14), // atht - frmt
(n14)-[:connect_to {distance: 11.2}]->(n15), // frmt - mlpt
(n16)-[:connect_to {distance: 5.1}]->(n18), // stcl - snyl
(n16)-[:connect_to {distance: 4.1}]->(n17), // stcl - sjs
(n16)-[:connect_to {distance: 7.4}]->(n19), // stcl - cptn
(n17)-[:connect_to {distance: 11.8}]->(n15), // sjs - mlpt
(n17)-[:connect_to {distance: 10.3}]->(n19), // stcl - cptn
(n18)-[:connect_to {distance: 9.9}]->(n15), // snyl - mlpt
(n18)-[:connect_to {distance: 3.3}]->(n19), // snyl - cptn
(n02)-[:connect_to {distance: 5.5}]->(n01), // <<==start reverse direction
(n18)-[:connect_to {distance: 2.9}]->(n01),
(n26)-[:connect_to {distance: 4.2}]->(n02),
(n14)-[:connect_to {distance: 17.1, linkType: 'bridge', toll: 5}]->(n26),
(n15)-[:connect_to {distance: 11.2}]->(n14),
(n18)-[:connect_to {distance: 5.1}]->(n16),
(n17)-[:connect_to {distance: 4.1}]->(n16),
(n19)-[:connect_to {distance: 7.4}]->(n16),
(n17)-[:connect_to {distance: 11.8}]->(n15),
(n19)-[:connect_to {distance: 10.3}]->(n17),
(n15)-[:connect_to {distance: 9.9}]->(n18),
(n19)-[:connect_to {distance: 3.3}]->(n18),
(n17)-[:train_to {distance: 4.0}]->(n16), // <<==start train
(n16)-[:train_to {distance: 5.1}]->(n18),
(n18)-[:train_to {distance: 2.9}]->(n01),
(n01)-[:train_to {distance: 5.5}]->(n02),
(n02)-[:train_to {distance: 4.2}]->(n26),
(n16)-[:train_to {distance: 4.0}]->(n17), // dropped 0.1 mile
(n18)-[:train_to {distance: 5.1}]->(n16),
(n01)-[:train_to {distance: 2.9}]->(n18),
(n02)-[:train_to {distance: 5.5}]->(n01),
(n26)-[:train_to {distance: 4.2}]->(n02),
(s01:School {name: 'Stanford University'}), // <<== add more places
(s02:School {name: 'Foothill Community College'}),
(s03:School {name: 'San Jose State University'}),
(s04:School {name: 'De Anza College'}),
(s05:School {name: 'Santa Clara University'}),
(a01:Airport {name: 'Mineta San Jose International Airport'}),
(n02)-[:has]->(s01), // <<== connect places to cities
(n01)-[:has]->(s02),
(n17)-[:has]->(s03),
(n19)-[:has]->(s04),
(n16)-[:has]->(s05),
(n17)-[:has]->(a01)找出所有有学校的城市
// find out all cities have school
MATCH (n:City)-[:has]->(m:School) RETURN n.name, m.name找到从帕洛阿尔托到圣克拉拉的最短距离
MATCH p = allShortestPaths((s {name: 'Palo Alto'})-[r:connect_to*..5]->(d {name: 'Milpitas'}))
RETURN NODES(p)找到从城市 A 到城市 B 的最短路线
MATCH p=(a {name: 'Palo Alto'})-[r*2..5]->(b {name: 'Milpitas'})
WHERE NOT(a-->b) // where a is not directly connected to b
WITH p, relationships(p) AS rcoll // just for readability, alias rcoll
RETURN p, reduce(totalDistance=0, x IN rcoll| totalDistance + x.distance) AS totalDistance
ORDER BY totalDistance
LIMIT 1我学到了什么?
-
这很有趣。
-
我应该使用 East Palo Alto 作为节点,而不是 Athertron (node-26)。
-
接下来需要做什么
-
研究 shortestPath 算法和更复杂的查询。
-
学习编写 API 和 Web UI 与服务器交互。
-
杂项
以下信息可能不属于此处,但我目前需要将它们都放在一个地方。由于我想在 Gephi 中使用图数据库,所以我需要导出数据。GraphML 是 Neo4j 和 Gephi 都通用的文件格式。我按照Lorenzo Speranzoni 的博客 - 如何将 Neo4Art 图数据库加载到 Gephi 中安装了工具,将数据导出到 GraphML 文件并导入到 Gephi 中。我计算了一些社交网络指标,如偏心度、接近中心性等,结果是有效的。
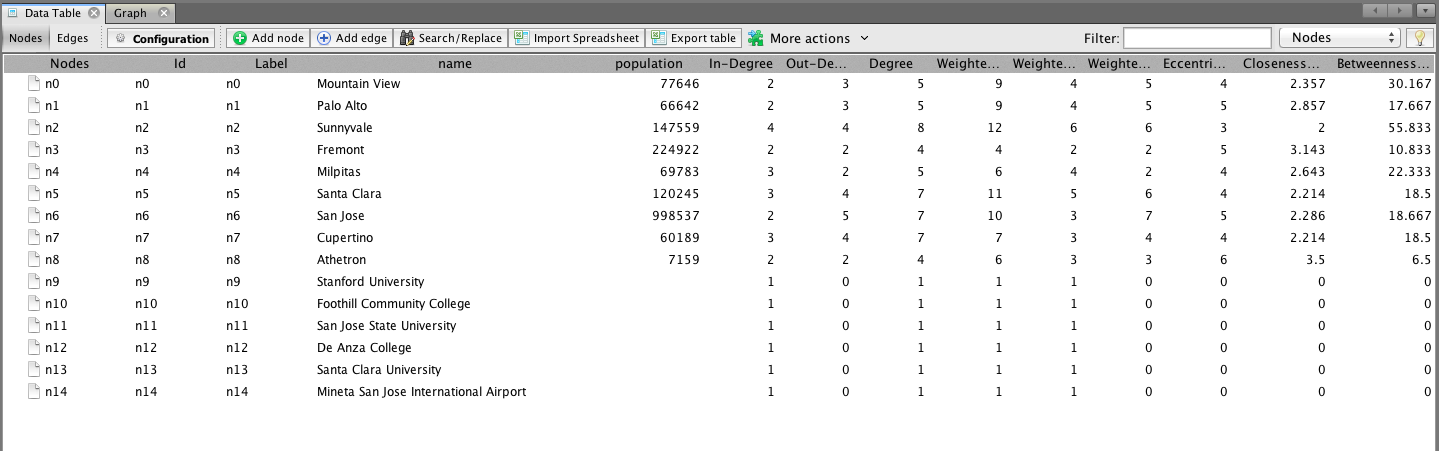
我安装了 Cytoscape 并导入了相同的 GraphML 文件,这也有效。非常好。
此页面有帮助吗?