使用 Neo4j 和 Cypher 进行多维图度量

此 Gist 的目标是演示我们在论文 Towards the characterization of realistic models: evaluation of multidisciplinary graph metrics 中收集的图度量。

数据集

例如，我们使用了一个简单的铁路网络，包括两条路线、三个路段、一个开关和三个传感器。

图 1. 铁路网络

此示例作为图的可能图形表示如下

图 2. 铁路图

此短视频演示了如何将铁路网络转换为图。

以下查询创建图（加载页面时会自动执行查询）。

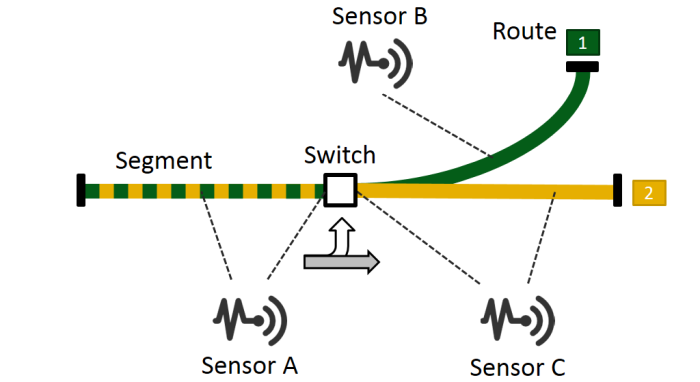
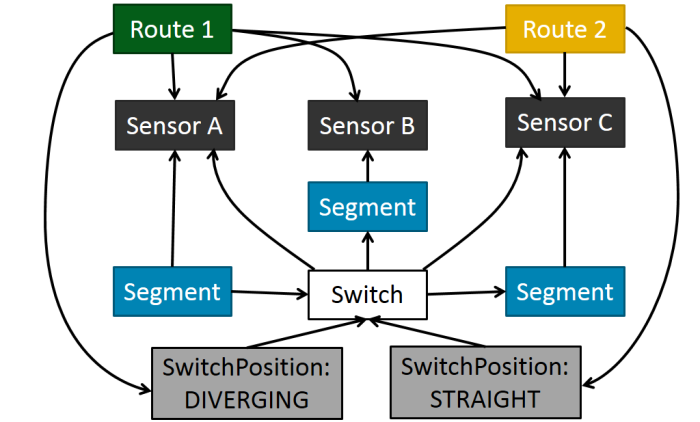
CREATE
  // nodes
  (route1:Route {name:"Route1"}), (route2:Route {name:"Route2"}),
  (sensorA:Sensor {name:"SensorA"}), (sensorB:Sensor {name:"SensorB"}), (sensorC:Sensor {name:"SensorC"}),
  (segment1:Segment {name:"Segment1"}), (segment2: Segment {name:"Segment2"}), (segment3: Segment {name:"Segment3"}),
  (sw:Switch {name:"Switch"}),
  (swP1:SwitchPosition {name:"SwP1", position:"DIVERGING"}), (swP2:SwitchPosition {name:"SwP2", position:"STRAIGHT"}),
  // requires edges
  (route1)-[:requires]->(sensorA),
  (route1)-[:requires]->(sensorB),
  (route1)-[:requires]->(sensorC),
  (route2)-[:requires]->(sensorA),
  (route2)-[:requires]->(sensorC),
  // monitoredBy edges
  (segment1)-[:monitoredBy]->(sensorA),
  (sw)-[:monitoredBy]->(sensorA),
  (sw)-[:monitoredBy]->(sensorC),
  (segment2)-[:monitoredBy]->(sensorB),
  (segment3)-[:monitoredBy]->(sensorC),
  // connectsTo edges
  (segment1)-[:connectsTo]->(sw),
  (sw)-[:connectsTo]->(segment2),
  (sw)-[:connectsTo]->(segment3),
  // target edges
  (swP1)-[:target]->(sw),
  (swP2)-[:target]->(sw),
  // follows edges
  (route1)-[:follows]->(swP1),
  (route2)-[:follows]->(swP2)

接下来，我们将介绍度量的正式定义，并使用 Cypher 查询在示例图上对其进行评估。有关符号的详细信息，请参阅论文。

一维度量

聚类系数

\(C(v) = \frac {\big| a, b \mid \mathit{Connected}(v, a) \land \mathit{Connected}(v, b) \land \mathit{Connected}(a, b) \big|} {\big| a, b \mid \mathit{Connected}(v, a) \land \mathit{Connected}(v, b) \big|}\)

MATCH (v)
OPTIONAL MATCH (v)-[r1]-(a1), (v)-[q1]-(b1)
WHERE a1 <> b1 AND r1 <> q1
WITH DISTINCT v, a1, b1
WITH DISTINCT v, toFloat(COUNT(a1)) AS possible

OPTIONAL MATCH (v)-[r2]-(a2)-[]-(b2)-[q2]-(v)
WHERE a2 <> b2 AND r2 <> q2
WITH DISTINCT v, a2, b2, possible
WHERE possible <> 0
WITH DISTINCT v, COUNT(a2) AS actual, possible
WITH v, actual/possible AS c
RETURN v.name, round(10^4 * toFloat(c))/10^4 AS c
ORDER BY v.name

多维度量

在维度-节点对上解释的度量

维度度

\(\mathit{Degree}\left(v,d\right) = \left|\big\{ w \in V \mid \mathit{Connected}(v, w, d) \big\}\right|\)

在维度上解释的度量

节点维度活动

\( \mathit{NDA}(d) = \big| \{ v \in V \mid \mathit{Active}(v,d) \} \big| \)

节点维度连接性

\( \mathit{NDC}(d) = \frac{\mathit{NDA}(d)}{|V|} \)

边维度活动

\( \mathit{EDA}(d) = \big| \{ (v,w,d) \in E \mid v,w \in V \} \big| \)

边维度连接性

\( \mathit{EDC}(d) = \frac{\mathit{EDA}(d)}{|E|} \)

MATCH (v)
OPTIONAL MATCH (v)-[e]-()
WITH
  toFloat(COUNT(DISTINCT v)) AS numberOfVertices,
  toFloat(COUNT(DISTINCT e)) AS numberOfEdges

MATCH (v)-[e]-()
WITH
  DISTINCT type(e) AS dimension,
  COUNT(DISTINCT v) AS nda,
  COUNT(DISTINCT v)/numberOfVertices AS ndc,
  COUNT(DISTINCT e) AS eda,
  COUNT(DISTINCT e)/numberOfEdges AS edc
RETURN
  dimension,
  nda,
  round(10^4 * toFloat(ndc))/10^4 AS ndc,
  eda,
  round(10^4 * toFloat(edc))/10^4 AS edc

ORDER BY dimension

在节点上解释的度量

节点活动

\( \mathit{NA}(v) = \big| \{ d \in D \mid \mathit{Active}(v, d) \} \big| \)

多路复用参与系数

\( \mathit{MPC}(v) = \frac{|D|}{|D| - 1} \left[ 1 - \sum\limits_{d\in D}^{}{\left(\frac{\mathit{Degree}(v,d)}{\mathit{Degree}(v,D)}\right)^2} \right] \)

MATCH (v)-[e]-()
WITH
  toFloat(COUNT(e)) AS degreeTotal,
  toFloat(COUNT(DISTINCT type(e))) AS numberOfDimensions

MATCH (v)-[e]-()
WITH v, type(e) AS dimension, COUNT(e) AS dimensionalDegree, degreeTotal, numberOfDimensions
WITH v, COLLECT(dimensionalDegree) AS dimensionalDegrees, toFloat(SUM(dimensionalDegree)) AS vertexDegreeTotal, degreeTotal, numberOfDimensions
WITH
  v,
  numberOfDimensions / (numberOfDimensions-1) *
  (1 - REDUCE(deg = 0.0, x in dimensionalDegrees | deg + (x/vertexDegreeTotal)^2)) AS mpc
RETURN v.name, round(10^4 * toFloat(mpc))/10^4 AS mpc

ORDER BY v.name

维度聚类系数

DC1 变体

\( \mathit{DC}_1(v) = \frac {\big| a, b \mid \mathit{Connected}(v, a, d_1) \land \mathit{Connected}(v, b, d_1) \land \mathit{Connected}(a, b, d_2) \land d_1 \neq d_2 \big|} {\big| a, b \mid \mathit{Connected}(v, a, d_1) \land \mathit{Connected}(v, b, d_1) \big|} \)

MATCH (v)
OPTIONAL MATCH (v)-[r1]-(a1), (v)-[q1]-(b1)
WHERE a1 <> b1 AND type(r1) = type(q1)
WITH DISTINCT v, a1, b1
WITH DISTINCT v, toFloat(COUNT(a1)) AS possible
WHERE possible <> 0

OPTIONAL MATCH (v)-[r2]-(a2)-[s2]-(b2)-[q2]-(v)
WHERE a2 <> b2 AND type(r2) = type(q2) AND type(r2) <> type(s2)
WITH DISTINCT v, a2, b2, possible
WITH DISTINCT v, COUNT(a2) AS actual, possible
WITH v, actual/possible AS dc1
RETURN v.name, round(10^4 * toFloat(dc1))/10^4 AS dc1
ORDER BY v.name

DC2 变体

\( \mathit{DC}_2(v) = \frac {\big| a, b \mid \mathit{Connected}(v, a, d_1) \land \mathit{Connected}(v, b, d_2) \land \mathit{Connected}(a, b, d_3) \land d_1 \neq d_2 \land d_2 \neq d_3 \land d_1 \neq d_3 \big|} {\big| a, b \mid \mathit{Connected}(v, a, d_1) \land \mathit{Connected}(v, b, d_2) \land d_1 \neq d_2 \big|)} \)

在维度对上解释的度量

每个节点v的节点活动二进制向量定义为

\( a_v = \left\{ a_v^{[1]},a_v^{[2]}, \dots, a_v^{[|D|]} \right\}, \text{where } a_v^{[d]} = \begin{cases} 1, & \text{if } \mathit{Active}(v,d),\\ 0, & \text{otherwise} \end{cases} \)

使用此向量，成对多路复用性度量为

\( Q(d_1, d_2) = \frac{1}{|V|} \sum_{v \in V} {a_v^{[d_1]} a_v^{[d_2]}} \)

MATCH (v)
WITH toFloat(COUNT(DISTINCT v)) AS numberOfVertices
MATCH (v)-[e]-()
WITH DISTINCT numberOfVertices,  type(e) AS d1
MATCH (v)-[e]-()
WITH DISTINCT numberOfVertices, d1, type(e) AS d2
OPTIONAL MATCH ()-[e1]-(v)-[e2]-()
WHERE type(e1) = d1 AND type(e2) = d2
WITH DISTINCT numberOfVertices, d1, d2, v
WITH DISTINCT d1, d2, COUNT(v)/numberOfVertices AS pairwise_multiplexity
RETURN d1, d2, round(10^4 * toFloat(pairwise_multiplexity))/10^4 AS pairwise_multiplexity
ORDER BY d1, d2

此页面是否有帮助？

GraphGists